Long term observations of the decametric Jupiter noise storms have shown that the likelihood of receiving these storms from Earth follows a roughly 11 year cycle with the high and minimum probabilities varying by perhaps as much as a factor of 10. This cycle is due to the Earth/Jupiter geometry as they orbit the Sun at different rates. The Earth, it seems, is much better positioned to receive the rather narrow beams of Jovian radio waves when it appears higher in Jupiter's sky. Imagine being on Jupiter and observing the Earth. Earth would have a set of right ascension and declination coordinates at which it would appear just as Jupiter does for us as Earthbound observers. The declination coordinate (analogous to latitude lines on the celestial sphere) of the Earth as it appears from Jupiter varies over the 11 year cycle we referred to above. This is called the Jovicentric declination of the Earth and is abbreviated De (called D sub e by Jupiter folks who have to say it a lot).
As it so happens the year 2000 is just about at the peak of this cycle and thus Jupiter has a good chance of being heard when other conditions are right. Unfortunately, this peak in De is also accompanied by a peak in the Sunspot cycle which means you are unlikely to ever hear Jupiter during the daytime because the ionosphere is made opaque by all that Sunspot activity. (On the up side again, this has turned out, at least so far, to be a relatively weak peak in the Sunspot cycle.)
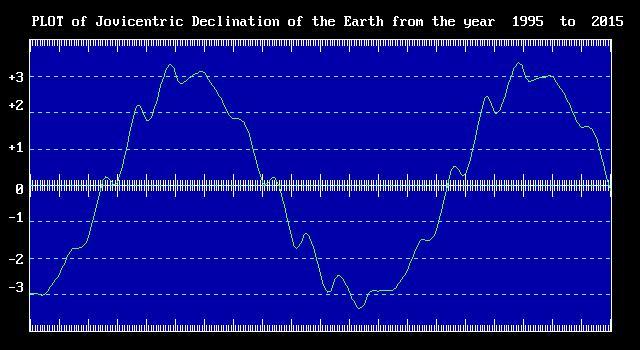
The graph below shows the De cycle from 1995 to 2015. The big tic marks on the horizontal scales represent years from left to right. The De varies from about minus 3.3 to plus 3.3 degrees. It is amazing that such a small angular shift makes such a big difference in our ability to hear Jupiter and it drives home the point that we are luck to fall within its radiation cones at all.

Looks like 2006 will be bad for hearing Jupiter so don't put off observing for too long!